هم‌نهشتی مثلث‌ها

تا حالا فکر کردین چرا بعضی شکل‌ها انگار کپی همدیگه‌ان، بدون اینکه دقیقا روی هم بیفتن؟ مثلا دو تا مثلث که هر گوشه‌شون یکیه، ولی ممکنه جای مختلفی باشن. اینجا پای یک مفهوم هندسی وسط میاد: هم‌نهشتی مثلث‌ها!

این اصل هندسی در خیلی از زمینه‌ها کاربرد داره؛ از طراحی سازه‌های مهندسی گرفته تا هنر و معماری. اگه کنجکاوی بدونی چطور با چند تا رابطه ساده میشه فهمید دو مثلث دقیقا مثل همدیگه‌ان، با ما همراه باش!

هم‌نهشتی مثلث‌ها یعنی چه

هم‌نهشتی مثلث‌ها یکی از مفاهیم پایه‌ای و کلیدی در هندسه‌ست که به مطالعه، تحلیل شکل‌ها و ابعاد اون‌ها می‌پردازه. این اصل بیان می‌کنه که دو مثلث هم‌نهشت هستن، اگه سه ضلع و سه زاویه‌ی یکی به ترتیب با سه ضلع و سه زاویه‌ی دیگه برابر باشه.

این تطابق می‌تونه از طریق چندین معیار مختلف اثبات بشه، از جمله: ضلع-زاویه-ضلع (SAS)، زاویه-ضلع-زاویه (ASA)، ضلع-ضلع-ضلع (SSS) و زاویه-زاویه-زاویه (AAA) که هر کدوم شرایط خاص خودشون رو دارن.

کاربرد هم‌ نهشتی مثلث‌ ها

در هندسه، هم‌نهشتی نقش مهمی در ساختارهای هندسی و اثبات قضایا داره. برای مثال، اگه دو مثلث هم‌نهشت باشن، میشه نتیجه گرفت که خواص اون‌ها، مثل مساحت و محیط، برابره. این ویژگی‌ها در مسائل مختلف مهندسی، معماری، هنر و زمینه‌های علمی دیگه کاربرد دارن.

بررسی هم‌نهشتی مثلث‌ها به دانش‌آموزان کمک می‌کنه که به درک درستی از اصول هندسه برسن و قدرت حل مسئله‌شون رو تقویت کنن. این مفهوم نه‌تنها پایه‌ی مباحث پیشرفته‌تر هندسه و ریاضیاته، بلکه باعث میشه دانش‌آموزان با اطمینان بیشتری سراغ چالش‌های پیچیده‌تر برن و راحت‌تر الگوهای پنهان بین شکل‌ها رو کشف کنن.

هم‌نهشتی مثلث‌ها فقط به کلاس درس و مسائل ریاضی محدود نمیشه؛ این مفهوم در زندگی روزمره هم کلی کاربرد داره. از طراحی الگوهای لباس و معماری گرفته تا مهندسی سازه‌ها و حتی هنر، این اصول هندسی بهمون یاد میدن چطور با دقت و ظرافت بیشتری جهان اطرافمون رو تحلیل کنیم و از نظم پنهان در شکل‌ها بهره ببریم.

هم‌نهشتی مثلث‌ها، به عنوان یک ابزار قدرتمند، به ما امکان میدن تا با دیدی وسیع‌تر به مسائل نگاه کنیم و راه‌حل‌های خلاقانه‌ای برای چالش‌های پیش رو پیدا کنیم.

اصول هم‌نهشتی

هم‌ریختی و هم‌شکلی دو شکل هندسی یعنی بتونیم اون‌ها رو مثل نسخه‌های متفاوت از یک طرح ببینیم. اما برای اینکه این شباهت رو به زبان ریاضی بیان کرده و دقیق‌تر بررسیش کنیم، از تعریف‌های مشخص و قضایای دقیق استفاده می‌کنیم. این قوانین بهمون کمک می‌کنن تا متوجه بشیم چه زمانی دو شکل واقعاً هم‌نهشت هستن و چطور می‌تونیم این رابطه رو اثبات کنیم.

به‌طور کلی، دو شکل رو زمانی هم‌نهشت می‌نامیم که مجموعه نقاط یکی از اون‌ها با یک تبدیل متقارن (Isometry) دقیقا به مجموعه نقاط شکل دیگه منتقل بشه. منظور از تبدیل متقارن، تغییریه که بدون دست زدن به اندازه ضلع‌ها یا زاویه‌ها، فقط شکل رو می‌چرخونه، جابه‌جا یا آینه‌ای می‌کنه. به بیان ساده‌تر، شکل‌ها دقیقاً یکسان می‌مونن؛ فقط موقعیتشون عوض میشه.

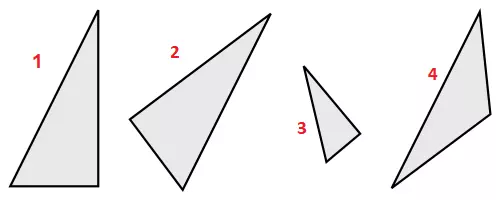
در این تصویر چهار مثلث ترسیم شده. دو مثلث سمت چپ با یکدیگر همنهشت هستن. مثلث سوم با مثلث‌های اول و دوم مشابه (Similar) است، ولی همنهشت نیست. از طرفی مشخصه که مثلث چهارم هم در اندازه اضلاع و هم زاویه با مثلث‌های دیگه متفاوته.

به بیان دیگه، میشه گفت اشکالی که به وسیله دوران، انعکاس یا جابجایی روی هم منطبق میشن، همنهشت هستن. در تصویر مشخصه که مثلث دوم رو با مقداری دوران (Rotation) و ایجاد تصویر انعکاسی (Reflection) و همچنین جابجایی (Translation) می‌تونیم روی شکل اول منطبق کنیم. هر یک از این تبدیلات رو که باعث همنهشتی مثلث‌ها در هندسه میشه رو مرور می‌کنیم.

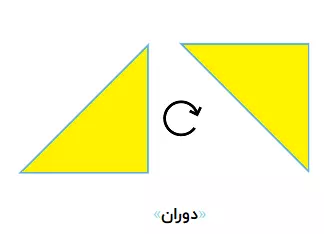
تبدیل دوران

دوران یا چرخش، یک حرکت دایره‌ای از یک تصویر در اطراف یک مرکز یا نقطه مرکزیه. در این تصویر دوران یک شکل رو مشاهده می‌کنین. همانطور که مشخصه فاصله بین نقطه‌ها و قالب شکل‌ها در کل، تغییری نیافته ولی نحوه نمایش شکل تغییر کرده.

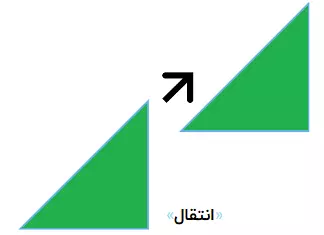
تبدیل جابه جایی یا انتقال

تبدیل جابجایی، عملیه که طی اون تمام نقطه‌ها به اندازه‌ای ثابت در جهتی خاص انتقال داده میشن. این تصویر نشانگر یک تبدیل جابجاییه که طی یک محور مستقیم نقاط تغییر یافته‌ هستن.

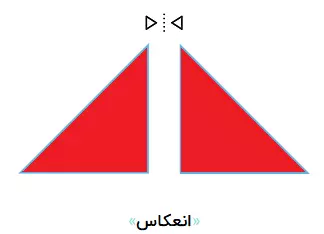
تبدیل انعکاسی

یک تصویر تبدیل یافته توسط یک تبدیل انعکاسی (بازتابی)، تصویر آینه اون در محور یا صفحه انعکاسه. همونطور که در این تصویر دیده میشه، خطوط قرمز رنگ به عنوان محور در نظر گرفته شده و شکل‌ قرمز، حول خط پایین، انعکاس داشته تا شکل سبز رنگ رو به وجود بیاره.

همچنین، انعکاس دوباره این شکل روی محور موازی با محور اولیه شکل آبی رنگ رو پدید آورده که با شکل قرمز رنگ معادله. این امر نشان میده استفاده از دو بار تبدیل انعکاسی روی یک شکل یکسان، دوباره شکل اولیه رو بازسازی می‌کنه.

تعریف هم‌نهشتی هندسی

در هندسه، دو شکل رو زمانی همنهشت میگن که بشه اون‌ها رو با استفاده از تبدیلاتی مثل دوران، انعکاس و انتقال روی یکدیگر منطبق کرد. به عبارت دیگه، اگه دو شکل در اندازه و شکل یکسان باشن، اون‌ها همنهشت هستن. این مفهوم در هندسه از اهمیت بالایی برخورداره؛ چون اساس خیلی از استدلال‌ها و اثبات‌ها در هندسه رو تشکیل میده.

هم‌نهشتی، یک رابطه‌ی اساسی در هندسه‌ست که بیان می‌کنه دو شکل می‌تونن در اندازه و شکل یکسان باشن، حتی اگه مکان یا جهت‌گیری اون‌ها متفاوت باشه. این مفهوم به ما اجازه میده تا اشکال هندسی رو بدون توجه به موقعیت مکانی یا جهت‌گیری اون‌ها، مقایسه و تحلیل کنیم.

هم‌نهشتی مثلث‌ها، پایه و اساس خیلی از مفاهیم پیشرفته‌تر در هندسه مثل تشابه، تقارن، و تبدیلات هندسیه. این مفهوم نه تنها در مطالعه‌ی اشکال دوبعدی بلکه در فضاهای سه‌بعدی و حتی در بعضی مفاهیم پیچیده‌تر مثل هندسه‌ی دیفرانسیل و توپولوژی هم کاربرد داره.

هم‌نهشتی مثلث‌ها

وقتی که طول ضلع‌های متناظر و اندازه زاویه‌های متناظر دقیقاً برابر باشه، دو مثلث هم‌نهشت هستن. یعنی اگه مثلث ABCABCABC با مثلث DEFDEFDEF همنهشت باشه، این رابطه رو با نماد زیر نشون میدیم:

ABC≅△DEF△

در خیلی از موارد، لازم نیست همه اضلاع و زاویه‌های دوتا مثلث رو بررسی کنیم تا بفهمیم همنهشتن. کافیه چندتا ویژگی کلیدی رو چک کنیم. توی فضای اقلیدسی، هم‌نهشتی مثلث‌ها با چهار حالت اصلی بررسی میشه:

1. ض-ز-ض (SSS): اگه سه ضلع متناظر دو مثلث برابر باشه، اون‌ها همنهشتن.
2. ض-ز-ض (SAS): اگه دو ضلع متناظر و زاویه بینشون برابر باشه، دو مثلث همنهشت هستن.
3. ز-ض-ز (ASA): اگه دو زاویه و ضلع بینشون برابر باشه، دو مثلث همنهشتن.
4. ز-ز-ض (AAS): اگه دو زاویه و یک ضلع غیرمشترک برابر باشه، دو مثلث همنهشت میشن.

این قوانین کمک می‌کنن بدون نیاز به بررسی تک‌تک اجزا، سریع‌تر تشخیص بدیم که دوتا مثلث دقیقاً مثل هم هستن یا نه.

یک نکته مهم اینه که اگه دوتا زاویه از دوتا مثلث برابر باشه، زاویه سوم هم حتماً برابره؛ چون مجموع زاویه‌های مثلث همیشه 180درجه‌ست. به همین خاطر، وضعیت AAS و ASA رو میشه معادل دونست.

حالت ویژه برای مثلث‌های قائم‌الزاویه:

• وتر و یک ضلع (RHS): اگه توی دوتا مثلث قائم‌الزاویه، وتر و یه ضلع متناظر برابر باشه، با قانون فیثاغورس میشه نشون داد که ضلع سوم هم برابره و بنابراین، دوتا مثلث همنهشتن.
• دو ضلع (HL): برابری دو ضلع، وقتی یکی از زاویه‌ها 90 درجه باشه، باعث هم‌نهشتی میشه.
• یک ضلع و ارتفاع وارد بر وتر: این هم یک حالت خاصه که توی مثلث‌های قائم‌الزاویه، هم‌نهشتی رو تضمین می‌کنه.

حواستون به این موارد هم باشه:

• AAA (سه زاویه برابر): لزوما هم‌نهشتی رو ثابت نمی‌کنه، فقط تشابه رو نشون میده.
• SSA (دو ضلع و یک زاویه): لزوماً باعث هم‌نهشتی نمیشه، چون ممکنه دوتا مثلث مختلف با همین شرایط وجود داشته باشه.

[inline_post_rel p_id=2088]

جمع‌بندی

در دنیای هندسه، هم‌نهشتی مثلث‌ها به ما یاد میده که چطور با بررسی چند ویژگی ساده، می‌تونیم به برابری کامل دو شکل پی ببریم. این مفهوم نه‌ تنها ذهن ما رو برای درک روابط پیچیده‌تر آماده می‌کنه، بلکه نشون میده که گاهی اوقات، شباهت‌های بنیادین حتی با چرخش یا جابه‌جایی هم از بین نمیرن.

یادگیری هم‌نهشتی، قدمیه برای شناخت نظم پنهان در جهان اطرافمون؛ نظمی که در کوچک‌ترین اشکال هندسی تا بزرگ‌ترین ساختارهای کیهانی وجود داره.

به پایان این مقاله رسیدیم و اگه دوست دارین در مورد بهترین روش تدریس ریاضی و اینکه چطوری ریاضی خودتون رو قوی کنین بیشتر بدونین، پیشنهاد می‌کنیم مقالات مربوط به این موضوع رو در وبلاگ پرش خوب مطالعه کنین.