انتگرالگیری یکی از بخشهای مهم و کاربردی ریاضیه که توی حل خیلی از مسائل علمی و مهندسی نقش مهمی داره. برای اینکه بهتر بتونیم این مفهوم رو درک کنیم، باید با فرمول انتگرال و روشهای مختلفش آشنا بشیم. این فرمولها ابزارهایی هستن که کمک میکنن مولفههایی مثل مساحت زیر نمودار و حجم اشکال سهبعدی رو به دست بیاریم یا حتی رفتار سیستمهای پیچیده رو تحلیل کنیم. اگه این فرمولها رو بلد نباشیم، کار کردن با مفاهیم پیشرفتهتر مثل معادلات دیفرانسیل یا فیزیک تحلیلی واقعاً سخت میشه.
خیلی از دانشآموزان این سوال رو در ذهن خودشون دارن که چگونه ریاضی خود را قوی کنیم؟. شاید به نظرشون یاد گرفتن فرمول انتگرال یک مقدار سخت به نظر بیاد؛ ولی باید گفت وقتی منطق هر روش رو بفهمیم، خیلی راحتتر میشه. مثلاً بعضی وقتها با یک تغییر متغیر ساده، مسئلهای که اولش پیچیده بود، سریع حل میشه. توی این مقاله قراره مهمترین فرمولهای انتگرالگیری رو بررسی کنیم، ببینیم هر کدوم کجا به درد میخورن و چطوری میشه راحتتر باهاشون کنار اومد. هدف اینه که این بخش از ریاضی برامون ملموستر و قابلفهمتر بشه.
البته اگه درگیر روزمرگیهاتون هستین و فرصت نمیکنین این مقاله رو به طور کامل بخونین، پادکست زیر رو گوش کنین و همراه رادیو پادکست پرش باشین❤🎧🔊
همه چیز درباره انتگرال و فرمولهای انتگرال گیری
انتگرالگیری یکی از پایهایترین مفاهیم ریاضیه که تو خیلی از مسائل کاربرد داره. با کمک فرمولهای انتگرالگیری، میتونیم چیزایی مثل مساحت زیر نمودار، حجم شکلهای سهبعدی یا حتی طول یک منحنی رو حساب کنیم. اگه مشتق، تغییرات لحظهای یک تابع رو نشون بده، انتگرال در واقع مجموع این تغییراته؛ مثلاً اگه سرعت لحظهای یه جسم رو بدونین، با گرفتن انتگرالش مسافت طیشده رو بهدست میارین.
کاربرد فرمولهای انتگرالگیری فقط به ریاضی محدود نمیشه. مهندسها ازش برای تحلیل نیروها و تعادل سازهها استفاده میکنن، فیزیکدانا برای محاسبه انرژی و کار روی سیستمها سراغش میرن و اقتصاددانها برای تحلیل سود و زیان یا پیشبینی رشد بازار بهش نیاز دارن. در واقع، هر جایی که یک کمیت بهمرور زمان تغییر کنه، انتگرال میتونه ابزار قدرتمندی باشه.
[inline_post_rel p_id=1718]
فرمولهای انتگرال گیری پایهای
برای اینکه بتونین از پس مسائل انتگرال بربیاین، باید اول فرمولهای انتگرالگیری پایه رو خوب یاد بگیرین. این فرمولها حکم آچار فرانسه رو دارن و کمک میکنن که توابع مختلف رو جزءبهجزء تحلیل کنین. مثلاً فرمولهای ساده زیر، یکی از اولین چیزهاییه که باید یاد بگیرین.
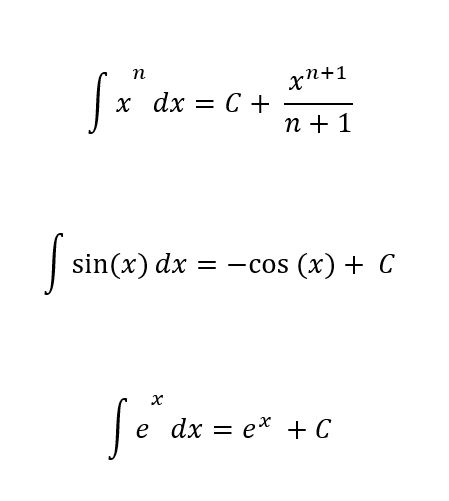
این فرمولهای پایهای نقش مهمی دارن، چون خیلی از مسائل پیچیدهتر رو میشه با تجزیه کردن به وسیله همین فرمولها حل کرد. وقتی این بخشها رو قشنگ درک کنین، حتی انتگرالهای سختتر هم مثل یک چالش شیرین به نظر میان. پس با تمرین کردن این فرمولهای انتگرالگیری، پایهتون رو قوی کنین تا بعداً راحتتر سراغ روشهای پیشرفتهتر برین.
یادتون باشه که در مواجه با این فرمولها، به هر میزان که شما بتونین با بهترین روش تدریس ریاضی آشنا بشین، میتونین روند بهتری رو در یادگیری این درس تجربه کنین.
پر کاربردترین فرمولهای انتگرال گیری در حل مسائل
یه سری فرمولهای انتگرالگیری هستن که خیلی جاها به کارتون میاد. مثلاً انتگرال توابع هیپربولیک یا کسرهای خاص، تو تحلیل سیگنالها، فیزیک و حتی آمار کلی استفاده میشه. یا فرمول گاوسی که توی نظریه احتمال خیلی مهمه و وقتی با توابع نمایی سروکار دارین، حسابی کمک میکنه؛ اما خیلی از اونها لزوما توی کنکور به کارتون نمیاد.
داشتن یه لیست از این فرمولها و دونستن کاربرد هر کدوم باعث میشه موقع حل مسئله سریعتر عمل کنی. اینجوری لازم نیست برای هر سوال از صفر شروع کنی؛ فقط کافیه ببینی مسئله شبیه کدوم فرمولهای انتگرالگیریه و مسیر حل رو سریعتر پیدا کنی.
انواع فرمولهای انتگرال گیری
فرمول انتگرال برای توابع کلی:
تابع در ریاضیات مانند ماشینی است که یک ورودی و یک خروجی دارد. هر تابع یک ورودی را به یک خروجی ربط میدهد.
فرمول انتگرال برای توابع گویا:
در علم ریاضیات هر تابعی که آن را بتوان به صورت کسری که صورت و مخرج آن تابع چند چملهای باشد، نوشت، تابع گویا نامیده میشود.
فرمول انتگرال برای توابع غیر گویا:
فرمول انتگرال گیری از لگاریتمها:
فرمول انتگرال گیری از توابع نمایی:
فرمول انتگرال گیری از توابع مثلثاتی:
فرمول انتگرال گیری از توابع هیپربولیکی:
فرمولهای انتگرال گیری از توابع معکوس هیپربولیکی:
فرمولهای انتگرال گیری از انتگرال های معین
قدم اول برای محاسبه یک انتگرال معین این است که بتوانید حاصل انتگرال را بدست آورید. باید از خودتان بپرسید چه تابعی وجود دارد که وقتی از آن مشتق بگیریم همین عبارت زیر انتگرال را به ما می دهد.
هر جوابی که به این سوال داده شود همان پاسخ انتگرال خواهد بود. اما باید در نظر داشته باشید محاسبه انتگرال ها همواره کار ساده ای نیست و بعضا لازم است از روش هایی مانند جزء به جزء، تغییر متغیر، تغییر متغیر مثلثاتی برای محاسبه انتگرال و …. استفاده نمائید.
انتگرال معین اصطلاحی است که به منظور محاسبه انتگرال در بازهای مشخص استفاده میشود. در حقیقت انتگرال معین، مساحت زیر منحنی در بازهای مشخص را نشان میدهد.
انتگرال چه کاربردهایی در زندگی و علوم دارد؟
«انتگرال کجای زندگی به دردم خورده؟» این جمله برای همه ما آشناست. اما برخلاف تصور برخی، انتگرال در بسیاری از علوم کاربرد دارد.
این مفهوم ریاضیاتی نخستین بار حدود 500 سال پیش به وجود آمده است و در ابتدا فقط برای محاسبه مجموع مساحت مورد استفاده قرار میگرفت.

از کاربردهای انتگرال میتوان به محاسبه مساحت اشکال مختلف اشاره کرد اما انتگرال در علوم مختلفی همچون جغرافیا، پزشکی، اقتصاد و هواشناسی کاربرد دارد.
برای مثال در علم پزشکی با استفاده از انتگرال و دیفرانسیل میتوان سرعت تغییرات مانند سرعت رشد تومورها را پیشبینی یا کنترل کرد. در علم اقتصاد هم، اقتصاددانان از انتگرال و دیفرانسیل برای به حداکثر رساندن سود و درآمد استفاده میکنند.
اگر این مقاله از مباحث ریاضی برای شما مفید بوده، توصیه میکنیم در رابطه با یکی دیگر از مباحث مهم ریاضی یعنی اعداد صحیح، طبیعی و گویا را در مجله آموزشی پرش، مورد مطالعه قرار دهید.
انتگرال را چگونه باید یاد گرفت؟
انتگرال گیری را تنها با حفظ فرمول ها می توانید یاد بگیرید.
روش انتگرال گیری از انتگرال های معین چیست؟
انتگرال گیری از انتگرال های معین فرمول هایی دارد که در متن بالا آمده است.
انتگرال در زندگی چه کاربردی دارد؟
برخلاف تصور این مبحث ریاضیات در علوم مختلف کاربرد دارد. برخی از کاربردهای انتگرال در متن آمده است.